1. はじめに

MEMSミラーはレーザーのスキャナとして古くより開発されてきた。現在では携帯型のレーザープロジェクタとして市販されている。また、車の自動運転に必要な距離画像を得るため、レーザーパルス光の反射時間を測定するライダー（LiDAR: Light Detection and Ranging）におけるレーザービームの走査にもMEMSミラーの利用が期待されている。しかし、ディスプレイ用のミラーでは、要求される解像度は高くなり（HDで横1920）、高い走査周波数も要求される。解像度を上げるためには、ミラー径と走査角を大きくする必要があるが、重いミラーとなり高い走査周波数の要求と矛盾する。また、ミラーの回転ねじればねの破壊限界も制限となる。ライダーにおいては、現在はディスプレイほどの解像度は要求されないので、前方用のライダーでは、ラスター走査できる低解像度ディスプレイ用ミラーを利用できる。レーザーパルスを同じミラーで受光する場合には、受光感度を上げるため、大きな径のミラーが必要で、大きな走査角も要求される。自動車では、厳しい耐久性と信頼性が要求されるので、振動の影響や破壊寿命の問題を解決することも不可欠である。本稿では、機械設計の基本から考え、上記の問題の限界と新しい取り組みを紹介したい。

2. 解像度とミラー径の関係

ミラー径は大きい方が、回折の効果が少ないので、物体の解像度はよくなる。LiDARの最大走査角（全光学角）θ_Optの中で分解できるスポットの数（解像スポット数）をNとして、目安はθ_Opt/Nがビームの回折広がり角D_OB/L（L:物体距離、D_OB:物体上のレーザースポット径）と等しくなればよい。厳密な回折と解像度Nの定義より、ミラーの直径をD、λを波長として、

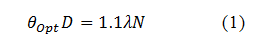
となる¹⁾。このように、光学的な制限から、分解能、走査角、ミラー直径、波長は関係付けられている。解像度を上げるには、大きいミラー径が必要である。
一方、ミラーの往復振動走査により、ミラー面は動的に変形する。変形の最大値δ_maxは、最大走査角のときに現れて、

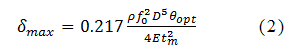
となる¹⁾。ここで、f₀ , t_m , E, ρは、それぞれ、走査周波数、ミラー板の厚さ、ミラーのヤング率と密度である。変形をλ/10以下に抑えなければ、変形により、スポット強度が下がりスポット形状が劣化する。変形δ_maxがミラーの径の5乗に比例しているので、高速走査ではミラー径の拡大は容易ではない。従って、変形を抑えるためにはミラーの厚さを厚くする必要がある。

3．運動非線形と破壊限界

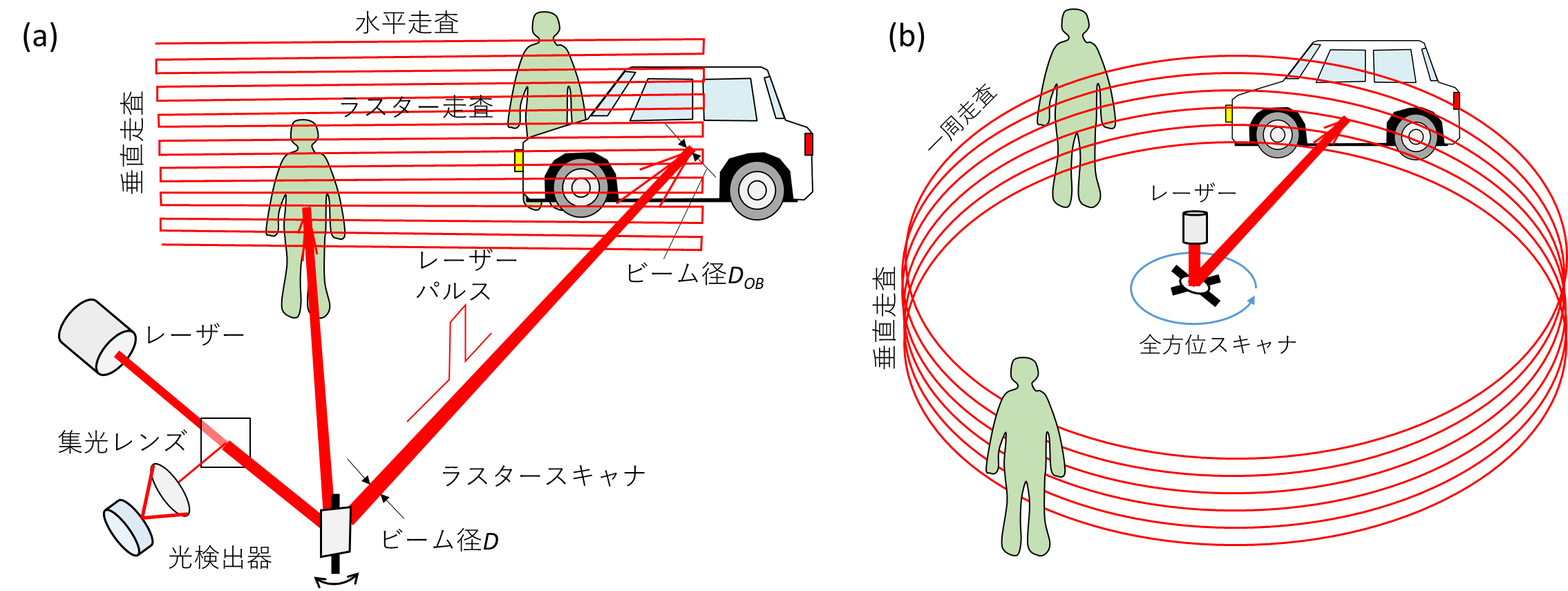
ディスプレイにおけるレーザーの走査には、2方向にミラーの角度を走査できる2軸のスキャナが用いられる。ライダーの走査においても、図1に示す2方式があり、ラスター走査（図1(a)）と全方位走査（図1(b)）である。どちらも2軸のスキャナを用いる。2軸スキャナの方式は、ジンバル型とジンバルレス型が研究されている。図2(a)、 (b)はそれらの基本構造を示している。ジンバル型は、1軸スキャナをジンバルフレームに組み込み、シンバルフレームをミラー軸に直行する軸で回転させる。ディスプレイ用のスキャナにはジンバル型のものが多い。ジンバルレス型のミラーは、曲げばねでミラーを支持し、ミラーを2軸に傾けて回転する。アクチュエータは対称に配置でき、配線等は容易になる。

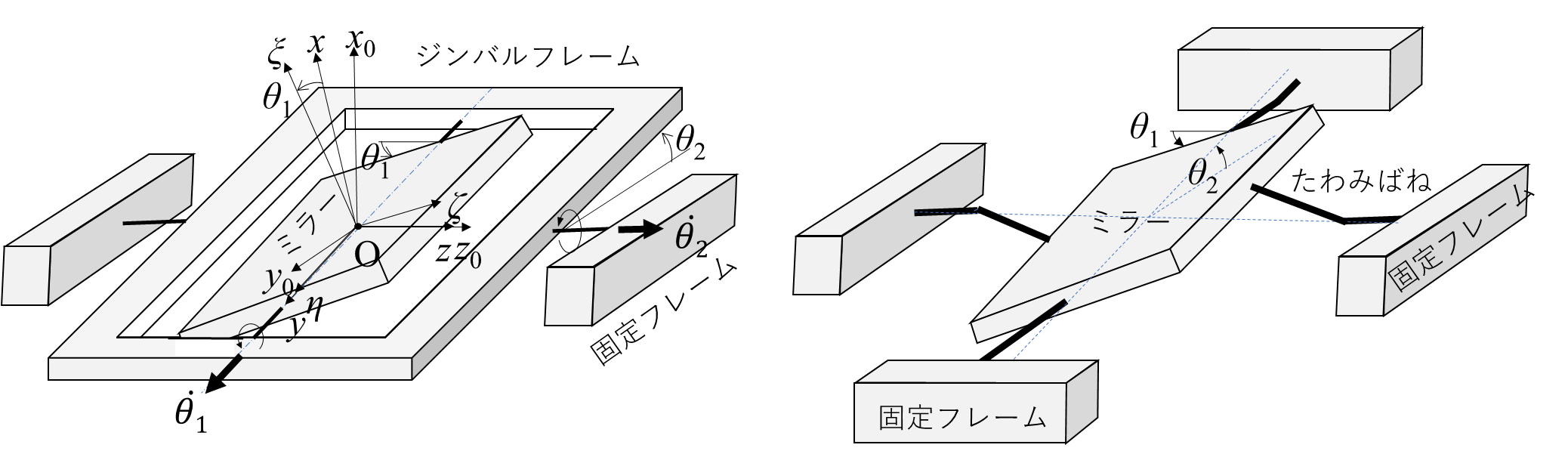
図2(a)において、ミラーはねじればねに支持されて往復回転振動する。回転角を増すため、一般には機械共振周波数f₀で走査する。ねじればねは、エッチングで製作されるので、断面は矩形である。簡単のため、ばねの断面を一辺の長さa の正方形とし、長さをℓとすると、材料の横弾性係数G(=61.5GPa(Si))を用いて、2本のねじればねの合計のばね定数は、

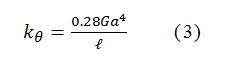
で与えられる²⁾。一方、シリコンの破壊の最大せん断応力τ_maxは最大光走査角θ_optのとき、ねじればねの幅の中央で発生し、

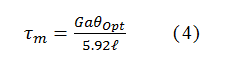
で与えられる²⁾（実際は、ばねの付け根部分に応力集中する場合が多い）。走査角は破壊応力の制限を受ける。共振走査周波数f₀は慣性モーメントI_θとばね定数k_θより2πf₀ = √(k_θ/I_θ)で与えられ、θ_optはf₀, I_θ, k_θ, γ_θにより与えられる。γ_θは運動方程式の減衰係数である。従って、解像度はγ_θが分かれば、周波数f₀と関係付けられる。図3にミラー直径Dをパラメータとして解像度Nの共振周波数f₀依存性の計算例を示した³⁾。ここで、計算において、λ =0.7μm, a =20μm, ℓ=150μm, ミラーの厚さ10μmとした。また、τ_m = 1.6GPaを用いた⁴⁾。

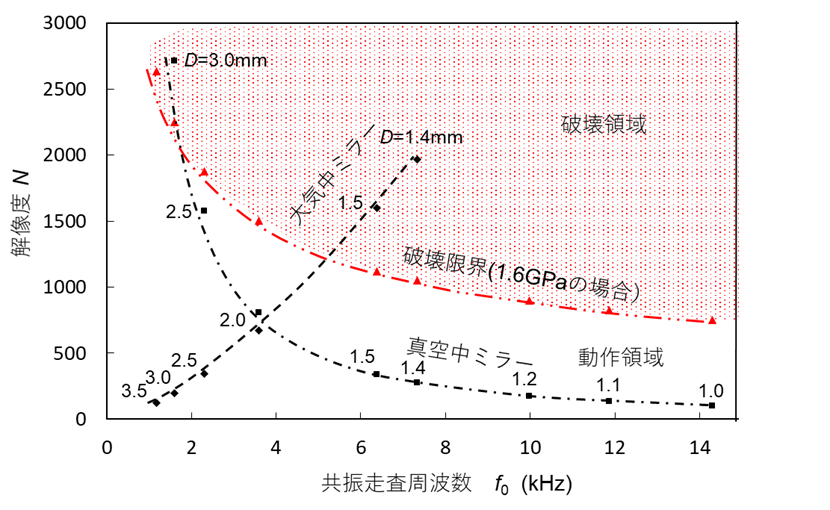
図3より、空気中と真空中でミラーを共振駆動させた場合、解像度の周波数依存性は全く異なることが分かる。空気中では、ミラー直径を小さくして、共振周波数を上げるように設計すると解像度は上がる方向に変化する。これはミラー径が小さくなって解像度が下がるよりも、ミラー径が小さくなって空気摩擦が減って回転角が上がる効果の方が大きいことによる。ミラーの径をあまり小さくしすぎるとこの関係は成り立たない。また回転角が大きくなってトーションバーの破壊限界に到達する。これらの兼ね合いでミラー径と解像度、共振周波数を決める必要がある。一方、真空中の共振ミラーの場合は、空気の摩擦がないので、大きいミラーの方が慣性は大きく、大きい角度が得られる。しかし大きい慣性のため、共振周波数は低下する。破壊限界の特性曲線と似た依存性を示すので、高解像度低速走査と低解像度高速走査のミラーを設計しやすい。実際には、走査ミラーのパラメータはいくつもあるので、いろいろな評価を行って最適の設計を行う必要がある。
次に、2軸ミラーの運動方程式を考える。ジンバル型において運動方程式を導出すると、θ₁、 θ₂ に関しての連立非線形方程式となる。空気摩擦等による減衰トルクを γ_{1 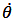1} 、 γ_{2 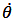2} （γ₁、 γ₂ は簡単のため定数）として加え、アクチュエータによる外力は、ミラーとフレームの軸 (η z) において、トルクN₁ 、 N₂とする。各軸の回転角 θ₁、 θ₂ の運動は以下の方程式で表される^5,6)。

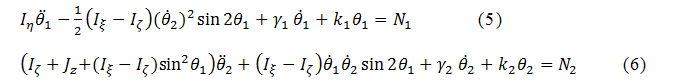
式(5)、 (6)より、ミラーとフレームの運動はこれらの方程式の第2項などにより、複雑に相互作用している。
ラスター走査の場合、フレームの周波数(角周波数ω₂)はミラーの周波数(角周波数ω₂)より2桁小さくω₂/ω₁<1/100であるので、ミラーの運動に対するフレームの非線形力の影響は小さいと思われる。一方、フレームの運動に対するミラーからの非線形力の影響は大きいが、フレームのゆっくりした運動に、早い周期的のミラーからの非線形力が加わるだけで、平均的なゆっくりした運動はあまり影響を受けないと思われる。従って、ラスター走査では、比較的安定な走査が行えると考えられる。
一方、図1(b)の全方向走査ではω₁ = ω₂であるので、ミラーの運動に影響するフレーム運動の非線形項はラスター走査の場合に比較して3～4桁大きいと考えられる。このように、全方向走査においては運動の非線形性がかなり強いと考えられる。ミラーの厚さが直径より十分小さい場合、共振周波数近傍の運転において、式(5)の第2項の最大値は、角度振幅 θ_mに対して、～k₁ θ_m³程度と見積もれるので、ばね定数k₁の反発力と組み合わせて、ばね定数は、おおざっぱにはk₁ (1-θ_m²) のように表せる。従って、ソフトスプリングのような非線形性を示すと考えられる。ここで注目される点は、もし、慣性モーメントI_ξ と I_ζ が等しい場合、これらの相互作用はなくなり、ミラーとフレームは、ほぼ独立に運動できると考えられることである。一般的には、2軸の回転の運動非線形が生じる。このため、ばねが線形であっても、非線形スプリングに似た振動が発生する。回転角速度に依存した相互作用力が発生して走査できる角度に制限が生じ、走査が楕円または不安定となる場合がある。

次回に続く－

【著者紹介】
羽根　一博（はね　かずひろ）
東北大学　大学院工学研究科　ファインメカニクス専攻　教授

■略歴
１９７８年３月　　名古屋大学工学部電子工学科卒業
１９８０年３月　　同大修士課程修了
１９８３年３月　　同大博士課程修了
１９８３年４月　　同大助手
１９８５年２月から１３ヶ月　　カナダ国立研究所物理部門客員研究員
１９９０年８月　　名古屋大学助教授
１９９４年４月　　東北大学教授