
先端データ企画部
部長 守屋 剛
1.はじめに
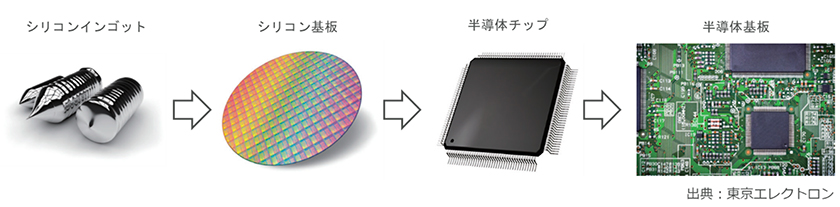
我々の生活には多くの電子機器が使われており、身近なところでは、自動車、スマートフォン、ドローンなど、数えれば限りがない。それら電子機器の心臓部である半導体デバイスは、シリコンから製造されている。半導体デバイスの製造は図1に示すような流れで行われる。シリコンインゴットから切り出されたシリコン基板に対して、さまざまな微細加工が行われて、半導体デバイスが製造される。ナノメートルオーダーの精度が求められ、薬液やプラズマなどを用いたエッチングや成膜プロセスが行われる。
半導体の加工は製造装置で行われ、さまざまな調整パラメータを用いて製造プロセスを制御している。機械学習を用いた新規材料の探索や製造プロセスの最適化について、さまざまな研究が行われており、コンピュータ性能が向上したことによって本格的に活用されるようになっている。1–4)
本稿では、半導体製造プロセスにおける機械学習技術の適用にフォーカスし、基本的な機械学習の理論について、プラズマプロセスなど複雑な系における条件最適化や材料スクリーニングの事例と、機械学習の基礎や技術的手法などを中心に紹介する。
2.機械学習を用いた半導体製造の最適化
人工知能(Artificial Intelligence:AI)とは、人間の知能をコンピュータ上で実現させる試み、あるいはそのための技術の総称のことである。時代や目的によって注目される技術が変遷するが、近年は深層学習(ディープラーニング)を含む「機械学習」を用いて様々な機能を実現させようという研究がなされている。
機械学習は、データ群に含まれる有用な知見を効率良く抽出するための技術である。図2に、機械学習の処理の流れを示す。機械学習アルゴリズムを用いて、様々なデータを学習することにより、規則や判断基準となるモデル式を自動生成する。このモデル式に基づいて、判定対象データを予測したり、分類したりすることができる。
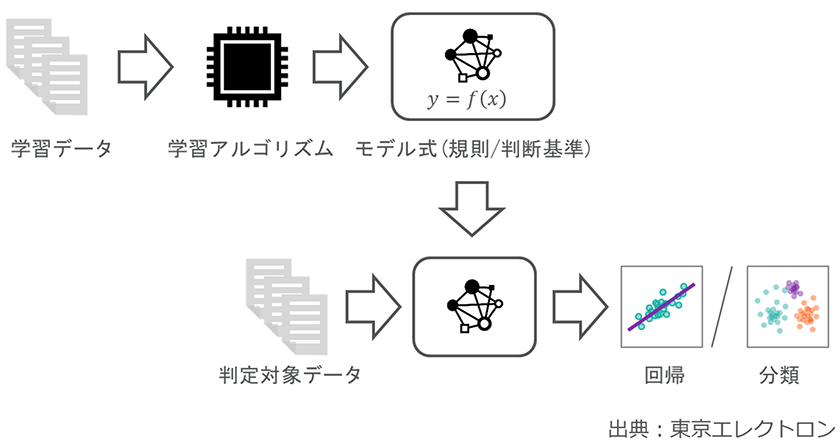
機械学習を用いることによる優位性として、大量のデータを処理できる、リアルタイムで処理できる、人間のスキルによらず高精度に処理できる、モデルを繰り返し利用できる、といったメリットが挙げられる。限られた少ないデータから推論するのは人間の方が得意であるが、十分なデータがあれば、機械学習は人と同等以上の精度で判断することが可能である。
代表的な機械学習は、未知の入力に対して出力を予測する「教師あり学習」とデータ自体の性質を抽出する「教師なし学習」とに分けることができる。教師あり学習には、ラベルを予測する「分類」と数値を予測する「回帰」がある。分類は、たとえば犬や猫の画像をラベル分けする目的で用いられ、回帰は、たとえば経時変化する金属疲労を予測し、装置の故障タイミングを予知することなどに用いられる。
表1に、代表的な分類、回帰アルゴリズムを示す。回帰アルゴリズムでは、観測データから関係式(モデル)を作成し、モデルを用いて未来の数値を予測する。新しいデータを取得した際、もしモデル式と合わなかった場合には、予測精度が悪いということになり、さらに多くの学習データを用いて、モデルの精度を上げる必要がある。一般に、データ量が多いほどモデルの精度が高くなるが、適切なモデルを作成するには統計の知識が必要となる。本稿で取り扱う、半導体製造プロセスへの機械学習適用では、主に回帰分析を行っている。
| 回帰 | 分類 | 説明 | |
|---|---|---|---|
| 線形回帰 | ✓ | 説明変数の係数と切片から連続値を予測する | |
| ロジスティック回帰 | ✓ | 線形回帰の出力をロジット関数に入力することで分類結果を予測する | |
| 自己回帰移動平均モデル | ✓ | 過去の値からの自己回帰や他の共通要素の移動平均を使って予測対象の時系列データを実績値のみから予測する | |
| 状態空間モデル | ✓ | 状態モデルと観測モデルを定義して、予測対象の時系列データをそれ以外の説明変数の時系列データから予測する | |
| k 近傍法 | ✓ | 未知データに対して、k個の学習データから最も近いものを選ぶ | |
| サポートベクターマシン | ✓ | ✓ | 各学習データ点からの距離(マージン)が最大となるような識別境界のパラメータを学習する |
| 決定木 | ✓ | ✓ | データと閾値を比較して段階的に分割するルールを木構造でモデル化する |
| ランダムフォレスト | ✓ | ✓ | 互いに独立決定木を大量に生成し、各々が異なる特性を持つように学習させ、各決定木の結果を集計して予測する |
| 勾配ブースティング | ✓ | ✓ | 生成済みの決定木が間違えてしまうデータを優先的に正しく予測できるように決定木を逐次的に増やす |
| ニューラルネットワーク | ✓ | ✓ | 複数のニューロンをつなげてネットワークを構成し、出力層での誤差が小さくなるように各ニューロン間の結合の重みを更新する |
3.プロセス最適化への機械学習の適用
機械学習においては、目的変数と説明変数を用いてモデル式を算出する。目的変数は、膜厚や膜応力などの目標値を意味し、説明変数は、半導体製造装置におけるプロセス条件などの設定値を表す。プロセス最適化の流れを図3に示す。
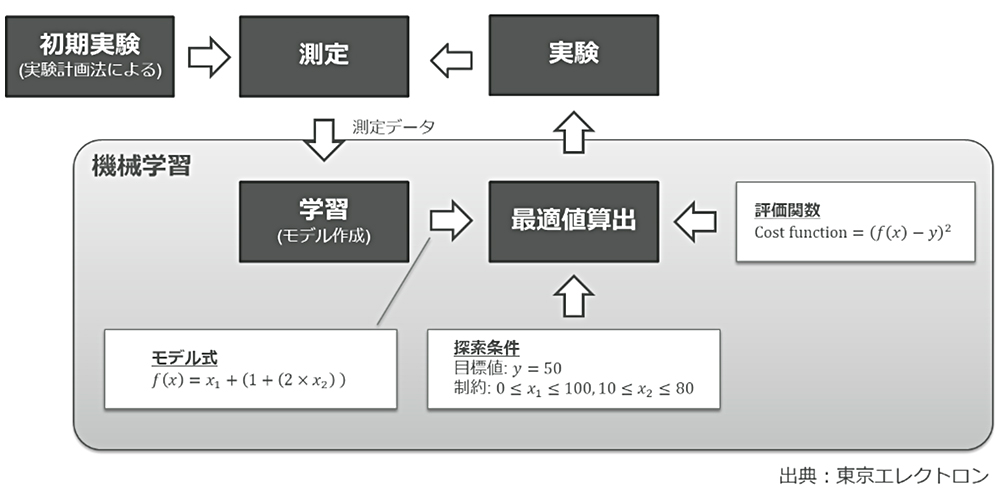
実験計画法によって初期実験データを取得し、測定データを機械学習し回帰モデルを作成する。モデル式に対して、目標値と制約を探索条件として、モデルから予測される最適値を算出する。その最適値でプロセス実験を行い、その結果をさらに機械学習させる。このループを目標値に到達するまで繰り返し実施する。
最適化において、モデル式と目的変数の目標値を入力し、その値を得るための推奨設定値を探索する。代表的な最適化アルゴリズムには、最急降下法と確率的勾配降下法がある。最急降下法は最適解を求める最も基本的な手法であり、現在位置における勾配を計算し、勾配が最も急な方向に進むことを繰り返すことで、最適解を求める手法である。一方、確率的勾配降下法はランダムサンプリングの手法をもちいて局所解を避けるようにした方法であり、深層学習でも頻繁に使われている。
半導体製造プロセスでは、たとえば、成膜速度と膜厚の均一性など、複数の目標を同時に最適化する必要がある。このような多目的最適化では、複数の目的関数に対して最適な結果を導くパラメータを求める必要がある。一般に、ある目的関数に対する最適解は、他の目的関数に対しては最適解ではないこと(トレードオフ)がある。このようなとき、パレート解を求めるという対応が行われる。複数存在するパレート解の中から適切な解を選択するのは人による判断に委ねられる。パレート解を求める手法としては、遺伝的アルゴリズムが代表的である。
発表文献
1) M. Hankinson, T. Vincent, K. Irani and P. Khargonekar, IEEE Trans. Semicond. Manufact. 10, 121 (1997).
2) S. Kang, IEEE Trans. Semicond. Manufact. 31, 149 (2018).
3) T. Tsutsui and T. Matsuzawa, IEEE Trans. Semicond. Manufact. 32, 428 (2019).
4) F. Tanaka, H. Sato, N. Yoshii and H. Matsui, IEEE Trans. Semicond. Manufact. 32, 444 (2019).
次回に続く-
【著者紹介】
守屋 剛(もりや つよし)
東京エレクトロン株式会社
先端データ企画部 部長
■略歴
1997年 日本電気株式会社入社
2001年 東京エレクトロン株式会社入社、現在に至る
2005年9月 広島大学大学院工学研究科博士課程修了(工学博士)
2008年3月 英国国立ウェールズ大学経営大学院修士課程修了(MBA)
■著書
戦略的CSRのススメ(共著、日新報道社)
超LSI製造・試験装置ガイドブック2009年版(共著、工業調査会)
クリーンルームにおける瞬低対策事例と装置(共著、日本工業出版)
