
取締役研究開発本部長
東北大学 名誉教授
山中 一司
1.はじめに
ガスセンサは環境と産業の安全と安心に不可欠なものであり、化学的センサ、電界効果トランジスタ(FET; field effect transistor)や電気抵抗型など電気的なセンサ、光学的センサなどがある。
しかし、これらのセンサは特定の物理的または化学的現象に基づいて、特定のガスの特定の濃度範囲でのみ使用できる。たとえば、触媒燃焼型水素ガスセンサは、爆発下限界(LEL)を超える水素濃度では水素が燃焼し、センサが爆発を誘起する可能性がある。一方、FETタイプの水素センサは、高感度である反面1〜10%を超えるガス濃度で飽和してしまう。水素ステーションや燃料電池自動車では、高圧水素容器の不具合により、低濃度の漏れだけでなく、急激に高濃度水素の噴出が起きる可能性がある。そこで広い範囲の濃度の水素のセンサが必要だが、まだ実現していない。
別の例として、ガスの微量水分の測定は、半導体プロセスや天然ガスのパイプラインシステムの品質管理にとって重要である。キャビティリングダウン分光法(CRDS)の水分検出限界は最も低いが、その用途は主に高純度ガス中の微量水分の検出に限定され、天然ガスのようにメタン、エタン、プロパンその他の重いガスで構成される混合中では適用困難である。鏡面ミラー型露点計は、長期安定性と再現性が高いが、微量ガスへの応答時間は長くなり、オンライン測定には適していない。
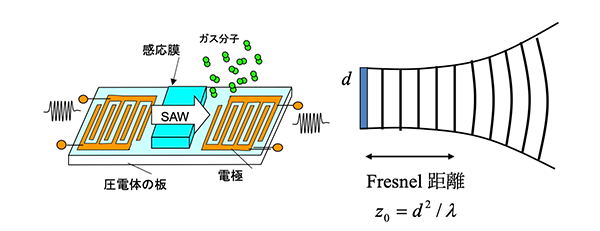
一方、スマホなど移動体通信用の周波数フィルタとしてSAW(Surface Acoustic Wave;弾性表面波)フィルタが普及している。図1のように、SAW伝搬経路上に感応膜を成膜してガスの吸着による音速減衰変化を測定するSAWセンサも研究され、弾性波と物質の多様な相互作用による高い汎用性が期待されている。しかし、SAWが一定の距離を超えて伝搬すると回折により拡散して減衰する。そこでSAWとガスの相互作用長が短いため感度に課題があり、SAWセンサの実用化は進んでいない。東北大学ではSAW素子の材料特性の計測法を研究していたが、あるとき軸受メーカーから、軸受球の表面傷のSAWによる検査の依頼を受けた。この検討中に、球のSAWを特定の条件で発生すると、回折によって拡がって減衰することなく、多重周回により長伝搬距離する現象が発見された。1) この現象がSAWセンサの飛躍的な感度向上をもたらす可能性に着目して、ボールSAWセンサ2,3) の開発が始まった。
本稿では、ボールSAWセンサの原理を説明する。また別稿で水素センサ、微量水分計およびガスクロマトグラフへの応用を紹介する。
2.無回折コリメートビームの発見
前節で述べた軸受球で観測したSAWの挙動が理論的に解析された。周波数が十分高く波長が球の直径より十分小さい場合は、図1(a)の座標系において、SAWの変位は
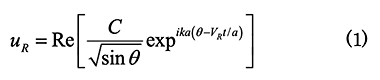
となる1)。ここで、C は定数、θ は発生点と観測点を結ぶ円弧の中心角(伝搬角)、k = 2π/λは波数(λは波長)、α は球の半径(kα は円周とSAWの波長の比)、VR はSAWの位相速度である。kα >>1の場合、VR は平面上のSAWの速度とほぼ等しい。
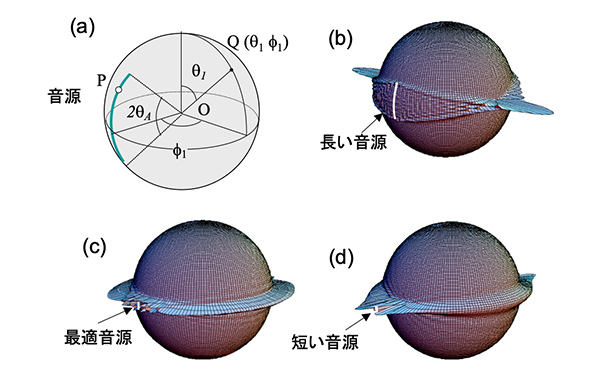
(a)解析に用いる座標系 (b)~(d)SAWのエネルギー分布の計算結果
式(1)は弾性波動方程式の解の球面上における展開の1次の項として導かれ、簡単であるが球面上のSAWの重要な特徴を表している。すなわち、平面上のSAWは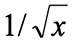 (xは音源からの距離)で幾何減衰項が与えられるが、式(1)では
(xは音源からの距離)で幾何減衰項が与えられるが、式(1)では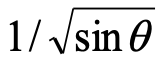 に置き換わっている。sinθ は伝搬角 θ の周期関数なので1周すると同じ値になり、幾何減衰は無くなる。また、発生点( θ =0°)から離れるにつれて振幅の減少したSAWが対極点で再び集まって、対極点( θ =180°)では無限大に発散する。
に置き換わっている。sinθ は伝搬角 θ の周期関数なので1周すると同じ値になり、幾何減衰は無くなる。また、発生点( θ =0°)から離れるにつれて振幅の減少したSAWが対極点で再び集まって、対極点( θ =180°)では無限大に発散する。
図2(a)の円弧状音源による球面上のSAWの伝搬が調べられた。音源上の点Pと観測点Qが中心となす角度を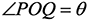 とおくと余弦定理より
とおくと余弦定理より
cosθ=cosφ0cosθ0cosφ1cosθ1+sinφ0cosφ1cosθ1+cosφ0sinθ0sinθ1 (2)
となる。中心Oから見た開口角が2θAの円弧状音源による点Qの音場は、式(2)に含まれる角度 θ0を独立変数にとって、式(1)の υRを – θAから θAまで積分することにより得られる。求めた音場の空間分布は、点Qの仰角 θ1の関数として表示する。
図2(b)は、波数パラメータkr=600の場合、円弧状音源から放射されるSAWのエネルギー分布を球面上に3次元的に表示した例である。球面からの高さがエネルギーを表わす。開口角2θA=60°の場合、伝搬角 φ1が増加すると音場の幅が減少し、φ1=90°で最小になった後、再び幅が増加して、対極点 φ1=180°で音源上と同じ分布が再現する。これは集束ビームである。これ以後は180°毎に同じ変化を繰り返し、何周回っても変化しない。この場合、音源の幅(開口角2θA=60°)より音場が広がることが無いので、θ1> θAの部分にはSAWのエネルギーが拡散しない。
次に、開口角が θA=2°と小さい場合、図2(d)のように、点音源の場合と類似した発散ビームとなった。伝搬角 φ1が増加すると音場の幅が増加し、φ1=90°で最大になった後、再び減少して、対極点 φ1=180°で音源上と同じ分布が再現される。集束ビームの場合と異なり、SAWのエネルギーが θ1 < θAの帯状部分に閉じ込められず、φ1=90°では、赤道から離れた位置まで広がる。支持部など接触部がこの近傍にあるとSAWは散乱される。そのため、このような状態は、球の精密な検査をする場合には好ましくない。ただし、無重力の場合や空気圧による球の浮上が行える場合は、支持部が無くて良いので、接触部による散乱の問題はなくなる。
最後に、図2(c)に示す開口角2θAがほぼ7°の場合、伝搬によって音場の幅はほとんど変化せず、常に θ1= θA程度の幅で伝搬するコリメートビームが得られた。このようなビームが得られる開口角をコリメート角 θ COLと呼ぶ。(b)-(d)を比較すると、開口角2θAがコリメート角 θ COLにほぼ等しいとき、最も狭い帯状部分にSAWのエネルギーが閉じ込められることがわかる。球にひずみや不均一性があっても、狭い軌道に閉じ込められたSAWの伝搬はあまり乱されない。支持部など接触部があっても軌道の外であればSAWは散乱されない。そこで、コリメートビームは最も減衰が小さく周回数が多いと期待される。
このコリメート角は波数パラメータkα に依存するので、kα を変化させて同様の数値解析を行った結果、表1のように変化した。コリメートビームの形成は、回折効果によって周辺に広がろうとする効果と球面の曲率による集束効果が拮抗した結果と解釈できる。表1の関係は、
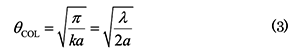
で精度良く近似できる。そこで、コリメートビームの幅wは近似的に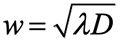 で与えられる。ここで、Dは球の直径である。式(3)は、ボールSAW素子において音源の長さを設計する際に有用で、異方性のある結晶の場合でも、電極形成位置の音速を用いて近似的に適用できる。結晶球での周回ルートは実験的に見出された。たとえば、LiNbO3にはいくつかの周回経路があるが、水晶やランガサイトでは、Z軸(Zシリンダー)に垂直な赤道に沿った経路の周回特性が最適である4)。ボールSAWに対する結晶異方性の影響は、三方晶結晶上の蛇行コリメートビーム5)など、まだ完全には理解されていない。
で与えられる。ここで、Dは球の直径である。式(3)は、ボールSAW素子において音源の長さを設計する際に有用で、異方性のある結晶の場合でも、電極形成位置の音速を用いて近似的に適用できる。結晶球での周回ルートは実験的に見出された。たとえば、LiNbO3にはいくつかの周回経路があるが、水晶やランガサイトでは、Z軸(Zシリンダー)に垂直な赤道に沿った経路の周回特性が最適である4)。ボールSAWに対する結晶異方性の影響は、三方晶結晶上の蛇行コリメートビーム5)など、まだ完全には理解されていない。
| 波数パラメータ kα | コリメート角 θCOL (Radian) |
|---|---|
| 50 | 0.28 |
| 160 | 0.15 |
| 320 | 0.10 |
| 530 | 0.075 |
| 790 | 0.065 |
次回に続く-
参考文献
- 1) Yamanaka K, Cho H and Tsukahara Y 2000 Precise velocity measurement of surface acoustic waves on a bearing ball Appl. Phys. Lett. 76 2797-2799.
- 2) Yamanaka K, Ishikawa S, Nakaso N, Takeda N, Sim, D, Mihara T, Mizukami A, Satoh I, Akao S, Ebi Y, Tsukahara Y 2006 Ultramultiple roundtrips of surface acoustic wave on sphere realizing innovation of gas sensors IEEE Trans UFFC 53 793–801.
- 3) 山中一司 2015 ボールSAWセンサを用いたガス中微量水分計測 応用物理 84, 218-223.
- 4) Akao S, Nakaso N, Ohgi T, Yamanaka K. 2004 Observation of the Roundtrips of Surface Acoustic Waves on a Single Crystal LiNbO3 Ball Jpn. J. Appl. Phys. 43 3067–3070.
- 5) Yanagisawa T, Ohgi T, Akao S, Nakaso N, Tsukahara Y, OharaY, Tsuji T and Yamanaka K Meandering collimated beam of surface acoustic waves on a trigonal crystal ball Appl. Phys. Lett. 98 123508.
【著者紹介】
山中 一司(やまなか かずし)
ボールウェーブ(株) 取締役研究開発本部長
東北大学名誉教授
■略歴
1975年 東京大学工学部物理工学科卒業
1977年 東京大学大学院工学系研究科修士課程修了(物理工学専攻)
1978年 通商産業省工業技術院機械技術研究所研究員
1987年 工学博士(東北大学)
1987年 カナダNRC工業技術研究所訪問研究員(兼任)
~88年
1997年 東北大学教授
2015年 東北大学名誉教授
2015年 ボールウェーブ株式会社取締役
現在に至る
超音波による材料評価・非破壊検査の研究および弾性表面波センサの研究に従事。1999年NEDOプロジェクトにて軸受球の非破壊検査の研究中に球の弾性表面波の自然なコリメートビームを発見、科学技術振興調整費研究にてボールSAW水素センサ、CRSETにて携帯型ガスクロを研究開発。1997年応用物理学会論文賞、2008年文部科学大臣表彰、山崎貞一賞受賞。東北大学名誉教授。
