
大木 眞一
1. はじめに
工業用流量センサは、流体の物理法則や機械的原理を応用して古くから社会で使用されている流量センサを継承して、様々な種類の製品が産業用途向けに普及している。本稿では、主な流量センサの種類と分類、選定方法、製品のコンセプトと設計の考え方、および代表的なアプリケーションなどについて述べる。
2. 流量センサの種類と分類
対象とする流体の流量・流速がダイナミック(動的)量であることから、温度、圧力のようなスタティック(静的)量に比べて測定が難しいため流体の種類、条件などに応じて適用可能な多種類のセンサが実用化されている。本稿で紹介する主な流量センサは歴史的に19世紀以来、開発、実用化され使用されている経緯がある。ここで主な流量センサの種類と分類を下記の3表の区分でまとめておく。
表1は、センサと流体との接触の有無、およびセンサの可動部の有無により分類した。表中に示すように、大半のセンサは測定流体に接触する接液形である。このため腐食性流体や付着性流体を測定する場合、材質を選択する必要がある。また可動部があるセンサは、長期間使用した場合に構成する部品の摩耗が懸念されるため定期的に校正することも検討する必要がある。
| センサと流体との接触 | センサの可動部 | センサの種類 |
| 接触する(接液形) | 可動部がある | 容積式、タービン式、面積式 |
| 可動部がない | 差圧式、電磁式、コリオリ式、熱式、 渦式、超音波式(接液形)、ピトー管式 |
|
| 接触しない(非接液形) | 超音波式(クランプオン形) |
表2は、流量を検出するために流体のエネルギーを利用するか、また測定原理、物理法則の応用の種別によりセンサを分類した。
流体のエネルギーを利用するタイプのセンサは、測定によって生ずるエネルギーの損失(流体が流れる管路内の圧力損失)が大きい。一方、流体のエネルギーを利用しないタイプのセンサはエネルギーの損失が小さいので省エネルギーの観点からは優位と言える。各種センサの測定原理は表中に示すように、物理法則を応用したタイプが多い。
| 流量を検出するために流体 のエネルギーを利用するか |
センサの種類 | 測定原理 物理法則の応用 |
|---|---|---|
| 利用する | 差圧式 | ベルヌーイの定理 |
| 容積式 | 容積の通過量を測定 | |
| タービン式 | タービンの回転数を測定 | |
| 面積式 | フロートの変位を測定 | |
| 渦式 | カルマン渦の原理 | |
| ピトー管式 | ベルヌーイの定理 | |
| 利用しない | 電磁式 | ファラデーの電磁誘導の法則 |
| 電磁式 | コリオリの原理 | |
| 熱式 | 熱の移動量を測定 | |
| 超音波式 | 超音波の伝搬時間差/ドップラーシフトを利用 |
表3は、測定流量・流速の区分、および適用流体によりセンサを区分した。
測定流量・流速の区分として、体積流量、質量流量、積算体積流量、および流速の4種に分類した。このうち積算体積流量とは、体積流量として一定の容積をはかり、その回数で積算した流量である。また流速センサはここでは、流体が流れる管内の1点を測定するピトー管のようなセンサとして分類する。各種センサの適用流体は、液体、気体、および蒸気の3種類の区分とした。なお流量センサを表中で区分したように、実用上体積流量、質量流量、および積算体積流量センサは流量計として使用される事例が多いので、以下の記述では各々流量計として扱う。
| 測定流量の区分 | センサの種類 | 適用流体 | ||
|---|---|---|---|---|
| 液体 | 気体 | 蒸気 | ||
| 体積流量 | 差圧式 | ○ | ○ | ○ |
| 面積式 | ○ | ○ | ○ | |
| 渦式 | ○ | ○ | ○ | |
| 電磁式 | ○ | × | × | |
| 超音波式 | ○ | ○ | △ | |
| 質量流量 | コリオリ式 | ○ | ○ | × |
| 熱式 | ○ | ○ | × | |
| 積算 体積流量 |
容積式 | ○ | × | × |
| タービン式 | ○ | ○ | △ | |
| 流速 | ピトー管式 | ○ | ○ | △ |
注)適用流体の区分:○ 適用可能 △ 使用上の制限あり × 適用不可を示す
センサの測定原理は、表4のようにまとめられる。
| センサの種類と測定原理、特長 | 測定原理図 |
|---|---|
| 差圧式流量計 差圧式は、最も歴史が長く使用実績が多い。 測定原理は管路を絞って、その前後に発生する差圧⊿pが流量の2乗に比例することから流量測定が出来る。 ベルヌーイの定理が成立して、流量Qを測定する。 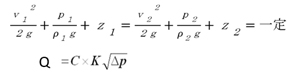 差圧を発生させる絞り機構の代表例として、オリフィス、ベンチュリ、ノズルなどがある。 |
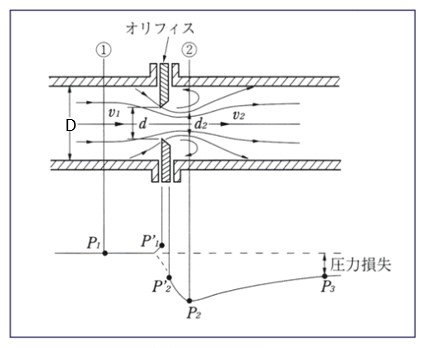 |
| 面積式流量計 面積式の測定原理は、管路の絞り部に発生する差圧を一定にし流量に応じて絞り面積を変化させる方式で、 フロートの位置で流量を測定する。古くから使用されており、構造がシンプルでコストが安い。 |
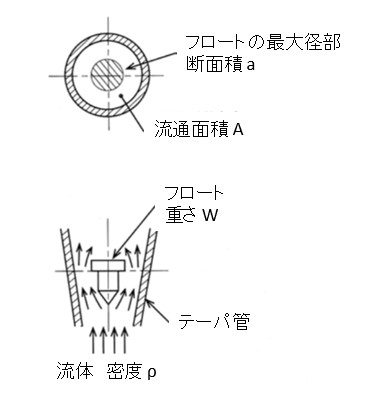 |
| 渦流量計 カルマン渦の原理を応用して流量測定に使用されている。 流れの中に設置された円柱の下流にb/a=0.281の関係で安定な2列の交番状の渦列が発生する。 発生する渦周波数fは、流速vと比例する。 ストローハル数Stは流体の種類によらず一定。 f=St・V/d 渦流量計は円管内に、流れに対向する位置に渦発生体を設置して流量測定する。 |
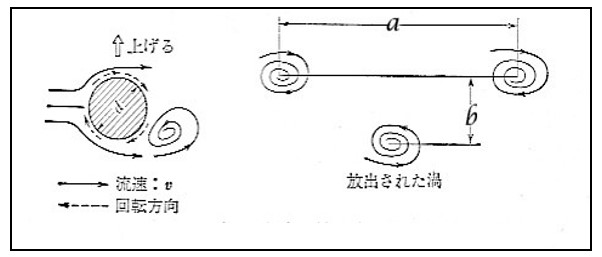 円柱の下流に生成されたカルマン渦列 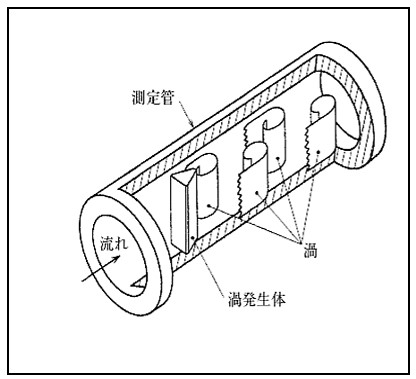 渦流量計の構造 |
| 電磁流量計 ファラデーの電磁誘導の法則を応用した測定方式。 センサ部の電極に発生する起電力Eが液体の流速vに比例する。 E=BDv 原理的に導電性がある液体流量を測定することが可能。 センサ部の測定管は絶縁体材料を使用しライニングで構成する。 |
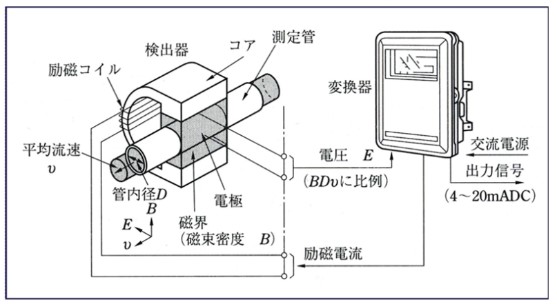 |
| 超音波流量計 超音波の伝搬時間差、またはドップラーシフトを利用した流量計。 伝搬時間差方式は、送受信器1、2間を伝搬する超音波の速度差から流体の流速を測定する。 流体中の音速Cとすると流速vが測定出来る。 V1-V2=2v・sinθ 超音波式は信号変換、演算部の技術開発が大きく進み、近年普及が拡大している。 小型軽量のポータブル形から大口径管路の測定用まで多くの用途がある。 |
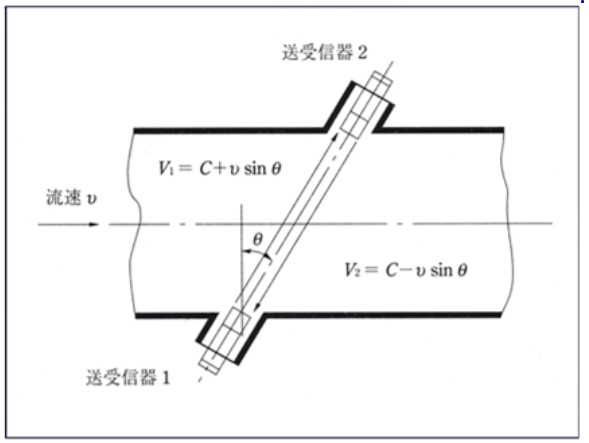 伝搬時間差方式の事例 |
| コリオリ式質量流量計 コリオリの原理を応用した流量計で質量流量を測定することが可能。 一定に加振されたU字管の上流側ではコリオリ力を受けて位相が遅れ、下流側では位相が進む。 このコリオリ力を受けて生ずる測定管の「ねじれ」を測定すれば質量流量に比例する。 コリオリ式は質量流量を高精度で直接測定することが可能。 |
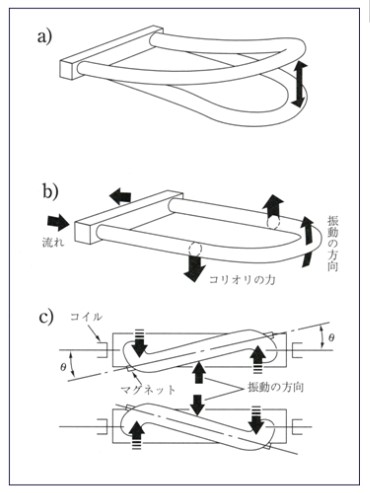 |
| 熱式流量計 主に気体用として使用され、中央部をヒーターで加熱した細管に気体が流れると、温度差ΔTが生ずる。 ΔTは質量流量に比例する。 微少流量を高精度で測定可能。 |
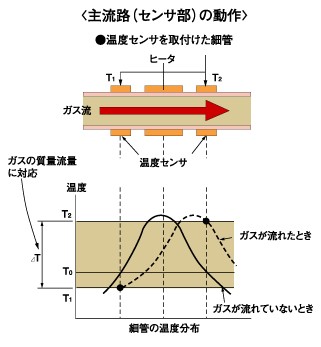 |
| 容積式流量計 一定容積の「ます」で流体を送り出し、その回転数を測る方式。 古くから使用されており、積算体積流量を高精度で測定可能。 |
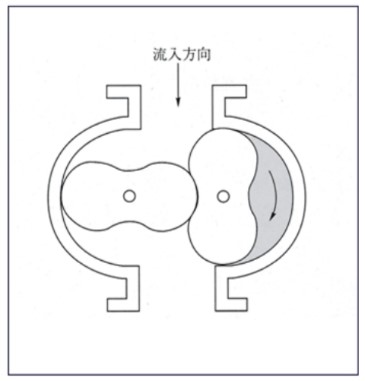 |
| タービン式流量計 回転軸に取付けた羽根車が、流速に比例して回転する方式。 容積式と同様に古くから使用され、高精度流量計および低コストの簡易形としても普及している。 |
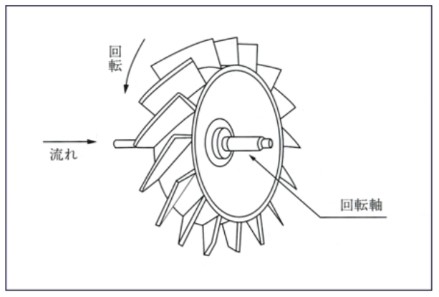 軸流羽車式の事例 |
| ピトー管式流速計 ベルヌーイの定理を応用した測定方式で、流速測定用として古くから使用されている。 管内の局所の流速を測定することにより、流速分布を測定する場合に便利。 P1、P2を測定することにより流速が測定出来る。 P2=1/2ρV2+P1 P2 -P 1=1/2ρV2 |
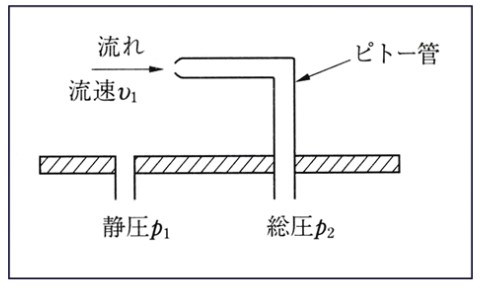 |
